![]()
宝瓶宮占星学 ―宝瓶宮時代の新しい西洋占星術―
ホロスコープとボーデの法則
―6数に秘められた宇宙哲理―
HOME > 宝瓶宮占星学―1.プロローグ > ホロスコープとボーデの法則
今回は占星学そのものではなく、ちょっと目先の変わったお話です。
惑星の位置を表したチチウス・ボーデの法則とホロスコープについてです。
太陽系の惑星配列とホロスコープ解読は切り離すことができません。
「ボーデの変形法則」なら海王星以遠にも当てはまる!

●第1稿 : 2009年4月23日アップ
●改訂稿 : 2022年 3月29日アップ
宇宙存在には「哲理」がある
●ギリシャ時代のアストロロジー(通称:古典占星術)には理論がありました
しかし、時代の発展とトランス・サタニアンの発見によって、現実への適応力を失っていったのです。
一方で、トランス・サタニアンを加えた昨今の現代西洋占星術は、木星の象意である高尚な精神性や哲学性を失い、海王星の象意である観念的な心理占星術やオカルト占星術(神秘占星術)に陥ってしまいました。
宝瓶宮占星学では、伝統的な占星学の流儀によって、ホロスコープ解釈の根拠を実際の宇宙の姿、すなわち存在様相におきます。
それは、科学的宇宙論や宗教的宇宙観をも含めた、統合的な「宇宙哲理」による解明です。
ここでは、ホロスコープの解釈や解読そのものには触れません。
なので、ホロスコープ解釈にしか興味のない人は、他のページに飛んでいきましょう♪
また、数字に弱い人には、ちょっと読みづらいかもしれません。ゴメンナサイ。(笑)
チチウス・ボーデの法則にある解釈を加えると、「ホロスコープ」解釈との共通性が見えてきたお話です。
《 存在の本質は、どんなカタチなの? 》
「ボーデの法則」にある解釈を加えた「ボーデの変形法則」とホロスコープ解釈の共通性をご説明する前に、必要な前振りから述べてまいります。
突然ですが、皆様に一つ ご質問を差し上げます。
宇宙の本質をカタチで象わすとすれば、どんなカタチだと思われますか?
三角形ですか?
四角形ですか?
ダイヤモンドのような多角形ですか?
それともカタチなんてない、と思われますか?
それぞれの観点によって、いろんな考え方があってもよいのですが、ポピュラーな観点からいえば、宇宙存在は「円」および「球」がその本質です。
もし、宇宙の本質が四角であれば、宇宙を構成する星は、「立方体」をしているはずですし、その軌道も四角く回っていなければなりません。
宇宙の本質が「円」ならびに「球」であるために、宇宙を構成する星々は球体ですし、その軌道も、楕円形を含めた円形を描いて半永久的に運動しています。
「円」や「球」が宇宙存在の最も自然なカタチであり、理想的な安定した姿なのです。
このことは人間自身にも当てはまります。
人間性や人格が理想的で立派な人のことを、「人格円満」と表現します。
「円熟した人」という言葉も類似の表現です。
また、トラブルや争いが、四方八方うまく解決した状態のことを「丸く収まる」といいます。
言動が自在で角が立たず、物事をスムーズに滞りなく進めることを「円転滑脱」といい、それを「円滑」と表現します。円や丸を使った表現の特徴は、理想の状態を意味しています。
One-Point ◆ 外国語の場合は知りませんが、日本人の霊性や英知が、「円」や「丸い」こと、また「球形」などが、存在の本質であることを感じとっていたようです。それゆえ「円」や「丸」を理想的な自然の状態として、このような言葉を使って表現するようになったのではないしょうか。
《 宇宙は6数および12数で閉じている! 》
さて、宇宙の本質が「円」や「球」であることを理解したら、一歩進んで、次のカタチを思い描いてください。
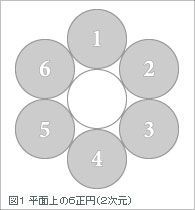
平面上(2次元)において、ある正円の周囲に同じ大きさの正円をぐるっと並べたとき、いくつ並ぶでしょうか?
ご存じのとおり、6個でピッタリと隙間なく並べることができます。(図1)
次は、立体(3次元)です。
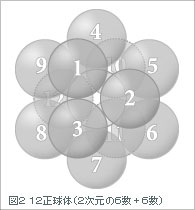
空間において、ある正球体の周囲に同じ大きさの正球体をぐるっと置いたとき、いくつ置くことができるでしょうか?
平面的に並べれば、6個置くことができますが、立体なのでその上下にも置かなければなりません。で、上に3個、下に3個置けます。
それゆえ答えは、12個になります。
図示(図2)すると複雑なので、あとで画像を掲載するかもしれません。
どうくっついているのかは、ビー玉などを13個用意して作ってみてください。
このとき、平面上に正円を並べたとき(図1)と同じ断面は、正四面体(正三角錐)を構成する面に平行して4方向にできます。
何をいいたいのかというと、ここに出てきた数字、2、3、4、6、12は、現代西洋占星術(占星学)を学んだかたなら、すぐにお分かりだと思いますが、「ホロスコープ」の解読に使われる数字と一致していることにお気づきだと思います。
ちなみに2は、6×2=12(12÷6=2)です。
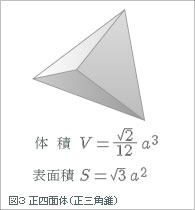
また、図3のように、正四面体(正三角錐)の体積や表面積の公式にも、2、3、12は使われています。
One-Point ◆何を言いたいのかというと、宇宙の本質が円や球であるために、それを最低限の個数で2次元や3次元に展開した場合、そこに2数や3数や4数、また6数や12数といったホロスコープで馴染みの数字が現われるということです。
「ボーデの法則」の検索はコチラ
●Google検索「ボーデの法則」
●Yahoo検索「ボーデの法則」
※「チチウス・ボーデの法則」や「ティティウス・ボーデの法則」で検索するよりも、「ボーデの法則」で検索したほうが、より多く引っ掛かります。
ヨハン・エレスト・ボーデ
●Johann Elert Bode,(1747.1.19-1826.11.23) ドイツの天文学者。
星座をギリシャ神話の画像で表したボーデの星座図「ウラノグラフィア」(1801)を出版。また天王星を発見したのはハーシェルだが、ウラヌスと命名したのがボーデ。
よっぽとウラヌスが好きだったのかも。(笑)
ボーデの星座図『ウラノグラフィア』の一部アンドロメダ。
《 チチウス・ボーデの法則とその「変形」 》
お待たせしました。(笑)
ここからが本題の「ホロスコープとボーデの法則」です。
正しくは、チチウスさんが発見し、ボーデさんが広めたために、「チチウス・ボーデの法則」(ティティウス・ボーデの法則とも)といいます。
略して「ボーデの法則」です。
(おいおい、チチウスさんは、どこにいったの?)
「チチウス・ボーデの法則」については、お手数ですが、皆様ご自身でフリー百科事典『ウィキペディア(Wikipedia)「ティティウス・ボーデの法則」などでお調べください。
同じことを書いてもしょうがないからです。
概要だけご紹介しておきますと、太陽系の惑星の距離に数理的な法則があるということを述べたものです。ケレス(セレス)の再発見や、天王星の発見に一役買ったようですが、海王星以遠の惑星(準惑星や小惑星を含む)には当てはまらないため、今では科学法則ではなく、経験則ということになっています。
ホントに?
で、ここからは、上の「ボーデの法則」をご理解した人のみお読みください。
理解していない人は読んでも分かりません。(笑) ウソです。
ご紹介したいのは、「チチウス・ボーデの変形法則」(勝手につけた名称)です。
この変形法則によって、太陽系の惑星の配列が、ほぼ当てはまってしまいます。
One-Point ◆ 「チチウス・ボーデの法則」は、2数、3数、4数を使って、惑星の距離を数式化しています。宇宙存在や森羅万象は、大まかに考えればということですが、単純な数字による数理によって表わされるということです。
「マケマケ」と「2002TC302」
●マケマケ
冥王星型天体、2005.3.31発見、直径1300-1900km、公転周期306.17年の準惑星(2005FY9)。
この近辺には、直径約1260km、軌道長半径43.5AUの準惑星クワオアーなど多くの小惑星があります。
●2002TC302
将来的に準惑星(冥王星型天体)に分類される可能性があります。
2002.10.9発見、直径420-1190km、公転周期410.65年。
ただし、軌道傾斜角35.04度の散乱円盤天体です。
「エリス」はサインの共鳴星か?
何かとお騒がせのエリスですが、正円かつ平面で、角度のみしか記さないホロスコープ的な認識では、エリスの本当の姿を見失います。
エリスは、かなり大きな楕円軌道を描いており、軌道は44度も傾いています。
黄道帯からは大きく外れているため、サイン(宮)との共鳴はありません。
実は、冥王星以遠の「冥王星型天体」は、いみじくも名称のとおり、「冥王星」(実はカロンとの二重惑星:未公認)が、共鳴星(西洋占星術では支配星)を代表しているのです。
●エリス(2003UB313)
冥王星型天体、2003.10.21発見、直径約2400km、公転周期559.55年の準惑星。近日点38.29AU-遠日点97.52AU、軌道長半径67.90AU、軌道傾斜角44.02度の散乱円盤天体。※参考:エリス軌道図
《 木星までのボーデの法則と土星以遠のボーデの法則 》
下の表をご高覧ください。
ボーデの法則は、(3×2n+4)÷10、つまり、0.3×2n+0.4 という数式で表わされます。
で、「チチウス・ボーデの変形法則」の場合は、分かりやすく、0.3N+0.4にして表現しています。変数Nが6数をもって乗数から等倍に変化するためです。
「遠6惑星」においては、変数Nの変化の仕方が変わることにご注目ください。
| 6 数 |
惑星 | チチウス・ボーデの法則 | 実際の距離 | 変形法則の場合 | |||
|---|---|---|---|---|---|---|---|
| 変数n | 計算値 | 変数N | 計算値 | 実際との誤差 | |||
| 近 6 惑 星 |
水 星 | − ∞ | 0.4 | 0.387 | 0 | 0.4 | 3.4% |
| 金 星 | 0 | 0.7 | 0.723 | 1 | 0.7 | 3.2% | |
| 地 球 | 1 | 1 | 1 | 2 | 1 | ― | |
| 火 星 | 2 | 1.6 | 1.524 | 4 | 1.6 | 5.0% | |
| ケレス | 3 | 2.8 | 2.767 | 8 | 2.8 | 1.2% | |
| 木 星 | 4 | 5.2 | 5.203 | 16 | 5.2 | 0.1% | |
| 遠 6 惑 星 |
土 星 | 5 | 10.0 | 9.555 | 32 | 10.0 | 4.7% |
| 天王星 | 6 | 19.6 | 19.22 | 64 | 19.6 | 2.0% | |
| 海王星 | 7 | 38.8 | 30.11 | 96 | 29.2 | 3.0% | |
| 冥王星 | 8 | 77.2 | 39.45 | 128 | 38.8 | 1.2% | |
| マケマケ | … | … | 45.43 | 160 | 48.4 | 6.5% | |
| 2002TC302 | … | … | 55.25 | 192 | 58.0 | 5.0% | |
※ n は、整数( number )または自然数( natural number )です。
※ 「計算値」や「実際の距離」の単位は、太陽から地球までの距離=1(AU)です。
※ 水星から木星までの近6惑星は、「ボーデの法則」どおり、2nで計算します。
※ 土星以遠の遠6惑星は、32ずつ加える32n=Nで「0.3N+0.4」を計算します。
One-Point ◆ 「チチウス・ボーデの法則」では、海王星以遠が該当しない…、ということでしたが、実は土星以遠からが変形法則であることが、この「チチウス・ボーデの変形法則」から分かります。そこには、6数において次元がステップアップするという、宇宙この世界の根本法則「宇宙哲理」、すなわち宝瓶宮時代のアストロロジー(通称:宝瓶宮占星学)が「基礎理論」とする宇宙この世界の「根本法則」につうじる法則があるのです。
《 ホロスコープとボーデの法則の共通性 》
繰り返しますが、水星から木星までの6つの惑星については、変数nは、「チチウス・ボーデの法則」どおりに、乗数によって変化していきます。
そこにおいては、変数N=2nで、「ボーデの法則」どおりです。
しかし、最初の6数(近6惑星)を超えて、次の次元の6数にあたる土星から太陽系外縁天体(冥王星型惑星)に至る遠6惑星においては、「チチウス・ボーデの変形法則」によって、土星の変数N(32)を基本に変数N=32nと等倍して変化していくことにご注目ください。
これは、乗数から等数加算、すなわち、最初の6数(次元)は乗数による「急激な展開」、そして次の6数(次次元)は等数加算による「安定した展開」ということです。
既存の「チチウス・ボーデの法則」には当てはまらなかった海王星も、この「ボーデの変形(2段階)法則」(笑)を使えば、ピタリと当てはまってしまいます。
お正月プレゼンツ「宇宙存在-人の生きる理由」や「ホロスコープとサインの真実」といった他のページで既にご紹介したとおり、「宇宙胎内システム」の連鎖によって、人類の「創造」と「成長」や「存続」が営まれています。
人間も、子どものときは急激な「成長発展段階」、成人後は緩やかな「安定成熟段階」へと移り変わっていきます。
これは人間だけではなく、宇宙の存在(成長発展の様相)、すなわち「宇宙哲理」がそうなっているからです。
これらを、「宇宙哲理」が秘められたホロスコープに展開すると、第一段階の6数が「個人」や「成長発展段階」を象わし、次の6数が「社会」や「安定成熟段階」を象わすということになります。
難しいですか?
占星術(学)を学んだり研究している人であれば、すぐにピンとくるでしょう。
こういった「宇宙哲理」を、「チチウス・ボーデの法則」や「チチウス・ボーデの変形法則」、また、ホロスコープの中に垣間見ることができるということです。
One-Point ◆ 分かりやすく書きましたが、実際は表面上の12数の中に、13数が含まれています。12数が13数を含むことによって、空間的な広がりや永続性が生まれていきます。詳細は、後日、述べることがあると思います。
西洋占星術の陥穽と混迷 ← BACK
NEXT → ホロスコープと配列の法則
※当ページの内容は著作権法により保護されております。無断使用はご容赦お願い申し上げます。
Copyright(C) 2005-2009-2022 Aquariun Astrology - Seiji Mitoma All rights reserved.