![]()
宝瓶宮占星学 ―宝瓶宮時代の新しい西洋占星術―
ホロスコープと配列の法則
―ケプラーの法則と動物の法則―
HOME > 宝瓶宮占星学―1.プロローグ > ホロスコープと配列の法則
宇宙存在や地上の存在には、どんな配列の法則があるのでしょうか?
まったくランダムに存在しているのであれば話は別ですが、
何らかの法則性があるのなら、ホロスコープの中にもそれがあるはずです。
サインやハウスと星の象意には法則がある

●第1稿 : 2009年5月13日アップ
●改訂稿 : 2022年 3月28日アップ
「万有引力の法則」の公式
●万有引力というのは、「2つの物体の間には、物体の質量に比例し、2物体間の距離の2乗に反比例する引力が作用する」というものです。
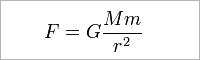
F:万有引力の大きさ
M.m:物体の質量
γ:物体間の距離
G:万有引力定数
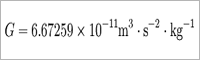
※う〜ん。難しいなぁ〜。(笑)
前のページの「ホロスコープとボーデの法則」に続いて、堅っ苦しいお話で申し訳ありませんが、「ボーデの変形法則」をご紹介したついでに、もう一つ小難しいお話を書いておきます。(^_^;)
多分、書いている本人もよく分かっていません。(笑)
その真偽はともかく、宇宙の星と地球の生物の配列に関するお話です。
《 万有引力とケプラーの法則 》
ニュートンが発見した「万有引力の法則」という名前を知らない人は、まずいないと思います。
現代物理学の基礎ともいえる法則なので、「リンゴが木から落ちるのを見て引力を発見した」と、エピソードを交えて義務教育で習わないことはありません。
正確には多分、発見というより、「気づいた!」ということだと思いますが、その数学的な公式となると門外漢には訳分かりません。
まあ、そんなことはどうでもいいのですが、このニュートンの「万有引力の法則」の基になったのが「ボーデの法則」と同じように経験則である「ケプラーの法則」です。
「万有引力の法則」は、ちゃんとした科学法則なので、その公式によって、ちょっとした微妙な惑星の軌道のズレから、その惑星に働く他の惑星の存在を計算して導くことができます。
ところが、「ボーデの法則」や、「ケプラーの法則」となると、科学法則ではなく経験則なので、「まあ、だいたいこんなもん」(笑=ご本人たちは真剣だと思いますが…)といったような大まかな概要を表わしていることになります。
One-Point ◆ もっとも、「ケプラーの法則」がなければ、ニュートンは「万有引力の法則」を発見できなかったでしょう。科学法則ではないとしても、「ボーデの法則」も「ケプラーの法則」も、他の意味で重要です。何でもかんでも科学で説明できるものが正しいわけではなく、現代科学では説明できない隠れた真実(哲理)もあるということです。
《 太陽系惑星はキレイに一直線上に並ぶ 》
「万有引力の法則」の話はともかく、ここで「ケプラーの第3法則」による太陽系の惑星の配列をみてみましょう。
下のグラフと表をご高覧ください。
「惑星の公転周期の2乗は、軌道の半長径の3乗に比例する」というのが、「ケプラーの第3法則」です。
平たくいえば、太陽から地球までの距離を1(AU)としたときに、太陽からある惑星までの距離を3乗すると、地球の公転周期を1(年)とした場合、その惑星の公転周期の2乗と同じになる、という配列の法則が宇宙(太陽系)には、あるということです。
それゆえ、各惑星は下のグラフのように一直線上に並んでしまいます。
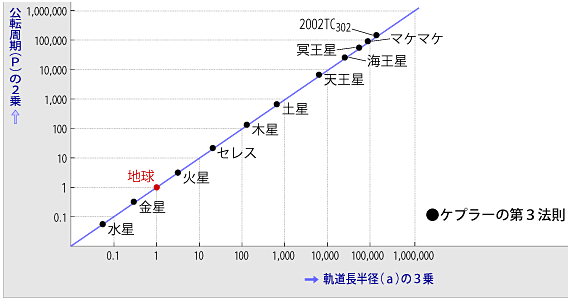
※上のグラフは、等数目盛ではなく、縦軸・横軸とも2乗や3乗した対数目盛です。
| 惑星 | 公転周期[年] (P) |
軌道長半径[AU] (a) |
公転周期[年] (P)の2乗 |
軌道長半径[AU] (a)の3乗 |
|---|---|---|---|---|
| 水 星 | 0.241 | 0.387 | 0.058 | 0.058 |
| 金 星 | 0.615 | 0.723 | 0.378 | 0.378 |
| 地 球 | 1 | 1 | 1 | 1 |
| 火 星 | 1.881 | 1.524 | 3.538 | 3.540 |
| ケレス | 4.600 | 2.766 | 21.16 | 21.16 |
| 木 星 | 11.86 | 5.203 | 140.7 | 140.9 |
| 土 星 | 29.46 | 9.555 | 867.9 | 872.3 |
| 天王星 | 84.02 | 19.218 | 7059.4 | 7097.8 |
| 海王星 | 164.77 | 30.110 | 27149.2 | 27298.1 |
| 冥王星 | 247.80 | 39.445 | 61404.8 | 61372.8 |
| マケマケ | 305.72 | 45.382 | 93464.7 | 93465.4 |
| 2002TC302 | 410.65 | 55.247 | 168633.4 | 168626.6 |
※上の表は、地球を基準「1」にして、公転周期や平均距離を計算した数字です。
※公転周期を2乗した数字と、平均距離(軌道長半径)を3乗した右側2列の数字(クリーム色の部分)が、ほぼ等しいことにご注目ください。
※ボーデの法則も、地球を基準にしたときに、2n といった対数による法則でした。
One-Point ◆ ケプラーは、「宇宙は無秩序であるはずはない、何らかの法則があるはずだ」と考えたようです。それゆえケプラーは、この法則を「宇宙の調和」と名付けました。ちょうど天動説から地動説への移行期で、ケプラーの法則は、地動説が正しいことの証明に大きく貢献しました。
ヨハネス・ケプラーの時代
●Johannes Kepler(1571年12月27日〜1630年11月15日)
コペルニクス(1473年2月19日〜1543年5月24日)が「天球の回転について」を、地動説と明言せずに発表した約100年後、ガリレオ(1564年2月15日〜1642年1月8日)は堂々と地動説を唱えました。
ケプラーは、このガリレオと同時代の人です。
ガリレオがケプラーに「地動説」に関する手紙を出したのが1597年。
その後、ガリレオは第1回裁判で有罪判決を受け、直後の1616年には地動説が禁じられます。
ケプラーが第3法則を発表したのは、その2年後の1618年でした。
ガリレオが『天文対話』を刊行したのは、さらに14年後の1632年。ケプラーは、すでにこの世の人ではなくなっていました。
ガリレオは、発刊後の翌1633年、第2回裁判で終身刑(後に軟禁)を受けます。
ちなみに、宝瓶宮時代の前史が始まったのが、1630年。双魚宮時代の25度の時点で、ここが新しい地平の黎明となります。→「宝瓶宮時代の根拠」
※宝瓶宮時代の0度(=双魚宮時代の30度)である「宝瓶宮時代のビックバン」は、1989〜1990年です。
《 地上の哺乳類もキレイに一直線上に並ぶ 》
次は、宇宙から地上に目を移して、哺乳類の体重[kg]と標準代謝量[W]の関係を見てみましょう。
こちらも同じく対数目盛によるグラフです。
こちらは、本川達雄著『ゾウの時間ネズミの時間』(中央公論社1992)という当時、話題になった本からの借用で、標準代謝量(E)[W]=4.1×体重(W)[kg]0.75 で表わされています。
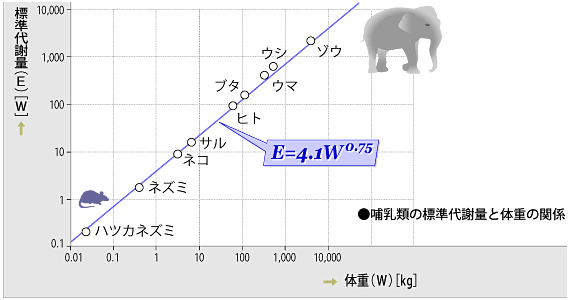
恒温動物の体重[kg]と代謝量[W]の関係は、体重が2倍、3倍と大きな動物になれば、代謝量も比例して2倍、3倍になるのではなく、実際には、3/4(=0.75)乗した分しか増えないということです。
例えば、体重が100倍の動物は、その代謝量は32倍にしかならないということです。
このほかにも、ゾウもネズミも心臓は、標準的に約15億回ほど打って止まる(寿命)ということがあるようです。
それゆえ、寿命の短いネズミは心拍数が早く、約15億回ほど打って止まるし、ゾウはゆったりと約3秒に1回と長く、約15億回ほど打って止まるために、ゾウのほうが寿命が長いという説です。
One-Point ◆ 先のページの「ホロスコープとボーデの法則」をはじめ、上の二つのグラフをご覧になればお分かりのように、宇宙の存在は、どうやら対数的な配列によって存在しているようです。科学法則というよりは経験則ですし、多少のブレやたまの例外はあるということは、宇宙の真実の一面なのでご理解ください。
サイン(宮)名は変更すべき?
●現代占星術では、春分点にはじまる最初のサイン(宮)を「牡羊宮」とし、以下、順番に黄道13星座の名前を流用してサイン(宮)名にしています。(蛇遣宮はありません)
ここに大きな間違いがあるのです。
星座とサイン(宮)は関係ないことが周知されれば、宝瓶宮時代のうちに他のサイン名を用いることになります。
そのほうが、占星学とは関係のない星座や星座名などに惑わされずに、正しくサイン本来の象意や配列を理解しやすくなるからです。
実際、今の星座名を流用したサイン名のままだと、約1万年後には、星座の位置とは、まったく正反対のサイン名を使うことになってしまいます。(笑)
《 それがホロスコープとどういう関係があるの? 》
皆さまは、上のグラフから何をお感じになられましたか?
何かを感じる・感じないは、皆さまのご自由なので、内容にまでは問いません。
ただし、ここは宝瓶宮占星学のサイトなので、占星学の観点から述べさせていただきます。
第一点は、ランダムに思える宇宙(太陽系)の惑星の配置には、法則があるということです。
第二点は、その法則は、宇宙の惑星のみならず、地上の生物にも類似の法則性があるということです。
第三点は、宇宙にも地上にも、法則性に基づく、配列や序列を見出すことができるということです。
皆さまは、いかが思われますか?
もちろん、先のページで取り上げた「チチウス・ボーデの(変形)法則」や、上に挙げた「ケプラーの第3法則」また「哺乳類の標準代謝量と体重の関係」といった法則だけが宇宙存在を象わす、すべての法則ではありません。
他の見方(切り口)をすれば、さらなる法則性が発見できるはずです。
そこで、重要なのは、ホロスコープとの関係です。
One-Point ◆ ドイツの天文学者ケプラーは、自然哲学者や占星術師としての一面を持っていました。当時は、小惑星やトランス・サタニアン(天王星、海王星、冥王星)の発見以前でしたが、「ケプラーの第3法則」は、その後に発見されたケレスやトランス・サタニアンなどにも見事に当てはまっています。
《 サインやハウスや星の象意にも法則性がある 》
現代では、パソコン上で星の配置が簡単に、しかも詳しく度数まで表示されます。
また、ハウスシステムを活用した三重円のホロスコープさえ、パソコンソフトによって一瞬で作成できてしまいます。
しかし、ケプラーの生存当時は、天動説と地動説の並存期ですし、コンピュータもありませんから、星の位置を正しく計算することさえ、手間隙がかかる不確定な作業だったはずです。
当然、星の象意の法則性にまでは意識が向かなかったことでしょう。
何を言いたいのかというと、宇宙にも地上の生物にも類似の法則性があって、何らかの配列や序列がみられるということは、宇宙の星の配置を写しとって、地上の出来事を解読するホロスコープにも、何らかの法則性があってまったくおかしくないということです。
占星学は、宇宙の星の配置や動きから地上の個人や人類の出来事をリーディングする、あるいは占うものです。
宇宙の星の配置や動きにも、法則性や配列があって、地上の生物にも類似の法則性や配列があるのです。
それらを結びつけるホロスコープの中にも、何らかの法則性や配列があるのは当たり前のことです。
天文学者であり、自然哲学者また占星術師でもあるケプラーは、時代状況ゆえに、星の位置を割り出すことに、まず力を注がなければなりませんでした。
もし、ケプラーがパソコンソフトで簡単に詳しいホロスコープが作れる現代に生きていたら、簡単にそのことに気づいたはずです。
サイン(宮)やハウス(室)や星(天体)の象意には、法則性や配列(序列)があるということに…。
One-Point ◆ それらを解き明かしたのが、通称:宝瓶宮占星学です。基礎理論の一つである配列(序列)法則がそれです。サイン(宮)やハウス(室)が無秩序な象意でもって牡羊宮から魚宮まで、また第1室から第12室まで並んでいるわけではありません。星の象意も同様で、配列に基づく意味、すなわち基本象意を持っているのです。
ホロスコープとボーデの法則 ← BACK
NEXT → 宇宙観とホロスコープ原論
※当ページの内容は著作権法により保護されております。無断使用はご容赦お願い申し上げます。
Copyright(C) 2005-2009-2022 Aquariun Astrology - Seiji Mitoma All rights reserved.